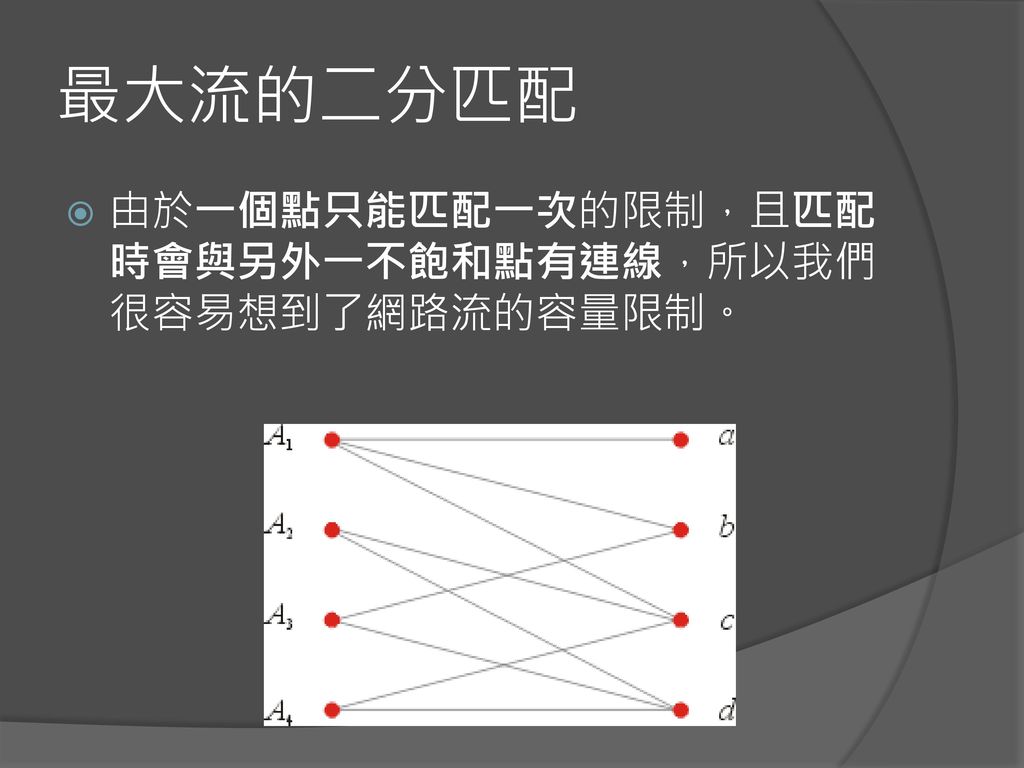
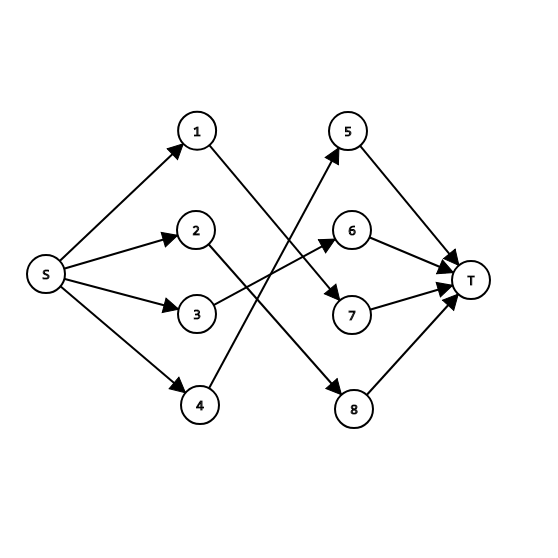
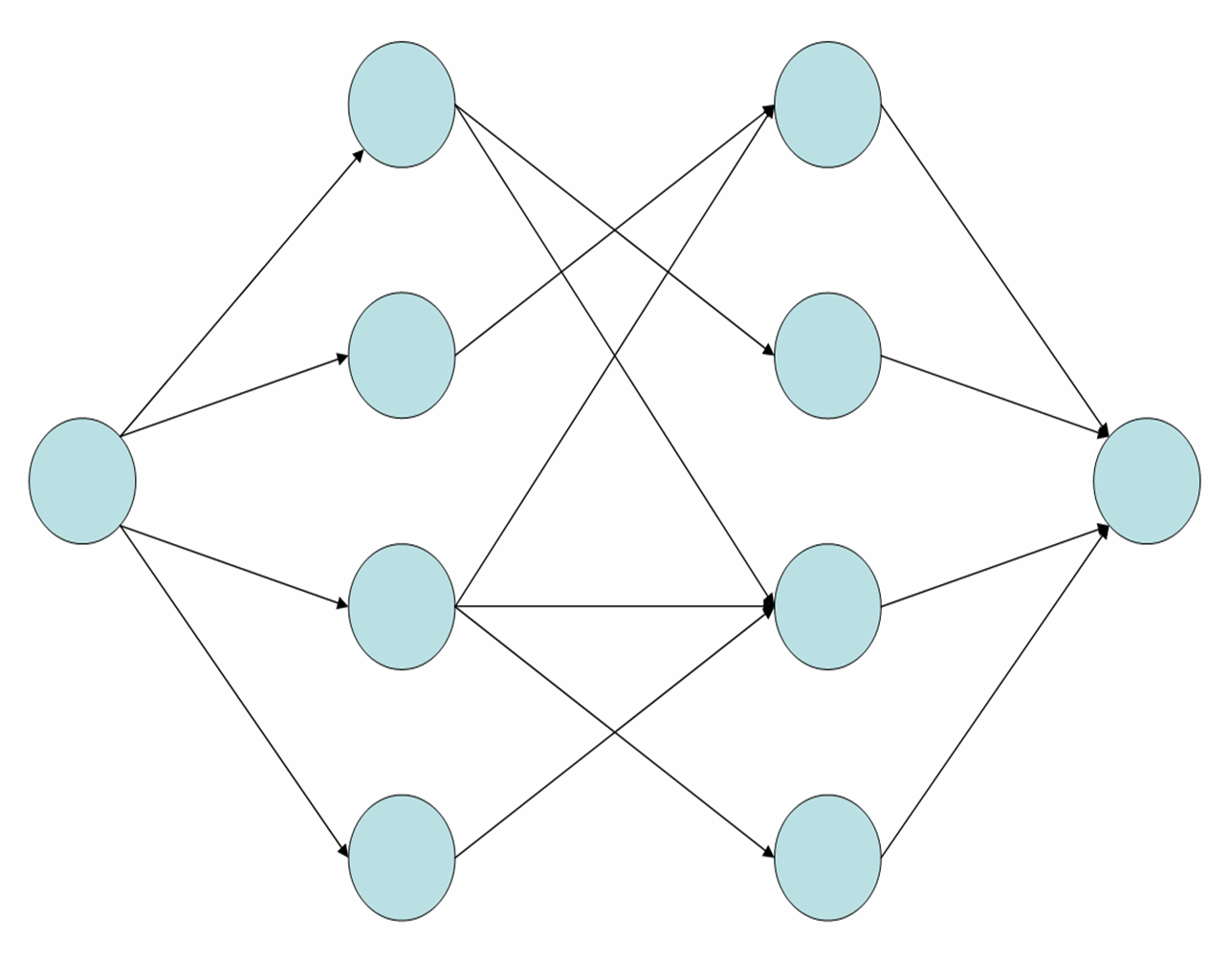
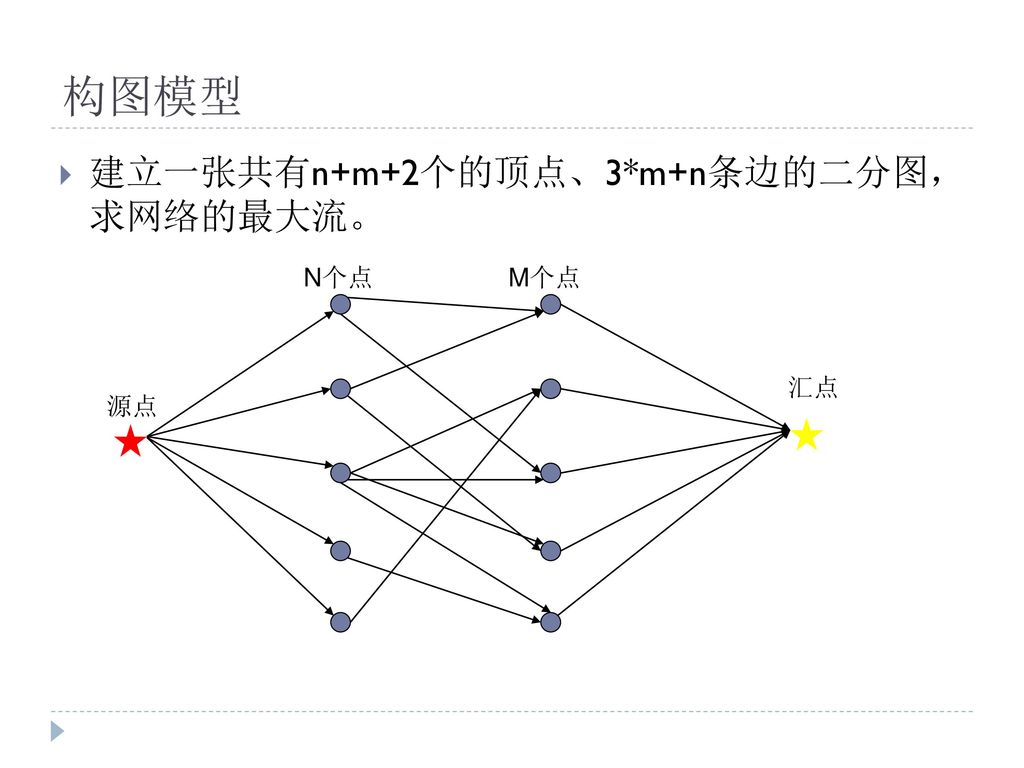
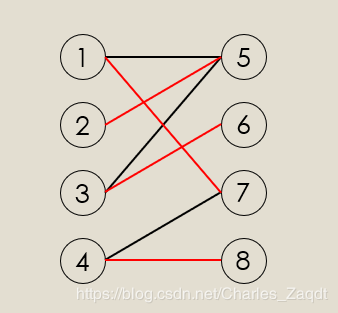
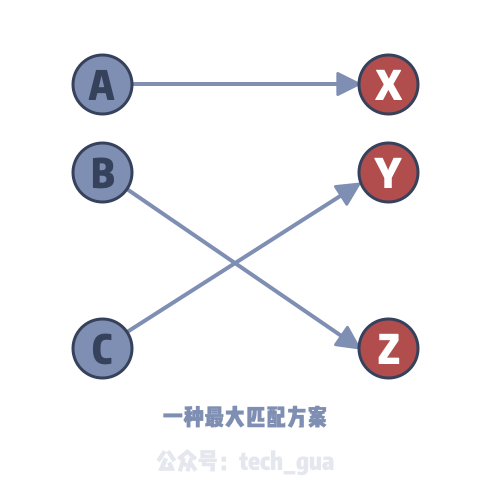
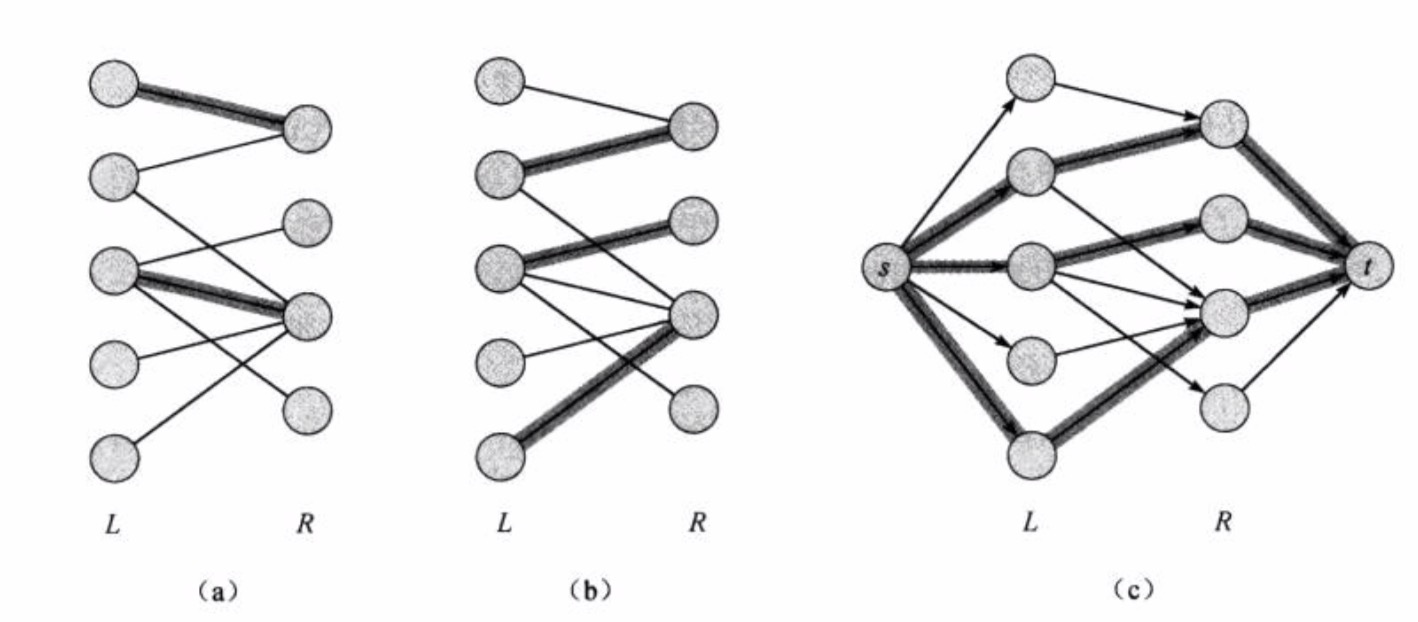
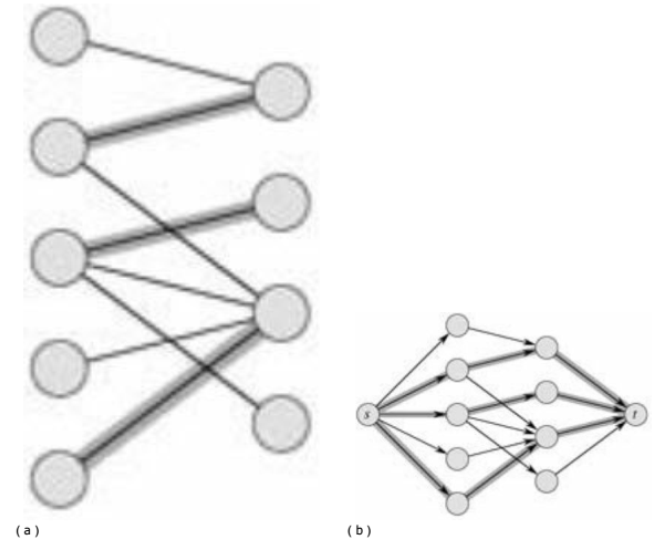
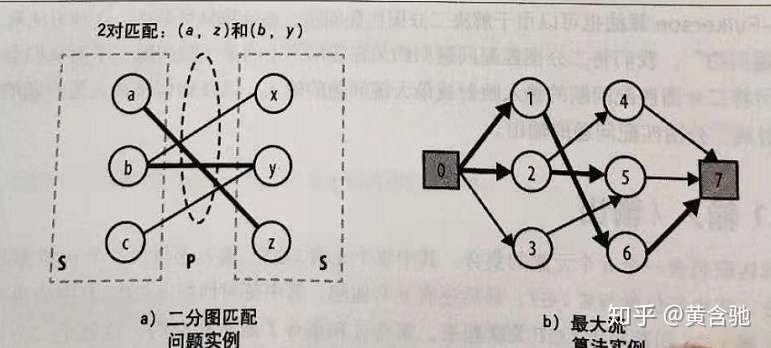
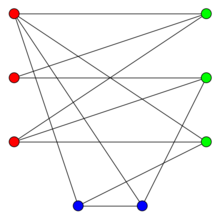
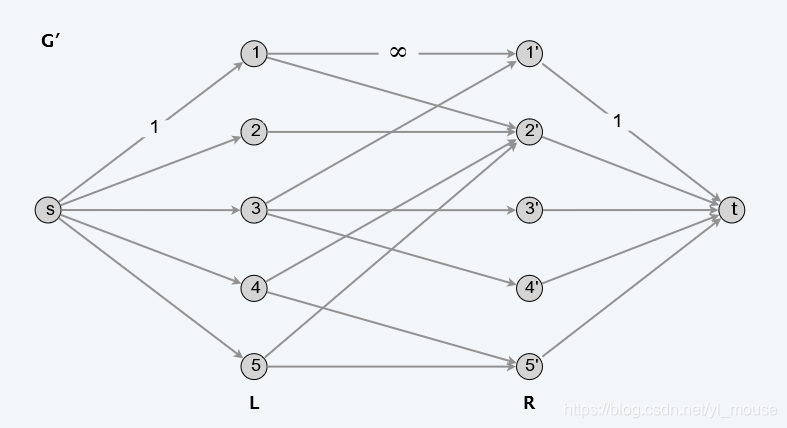
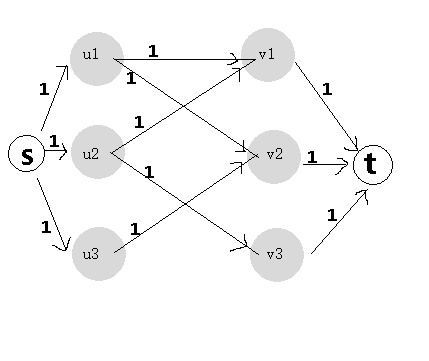
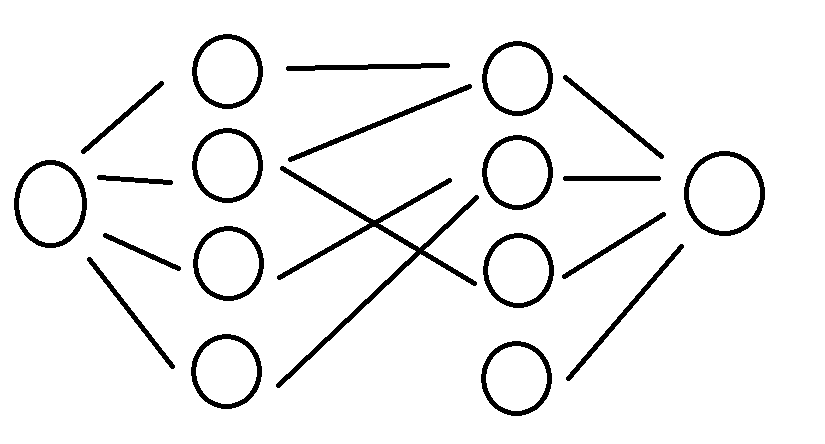
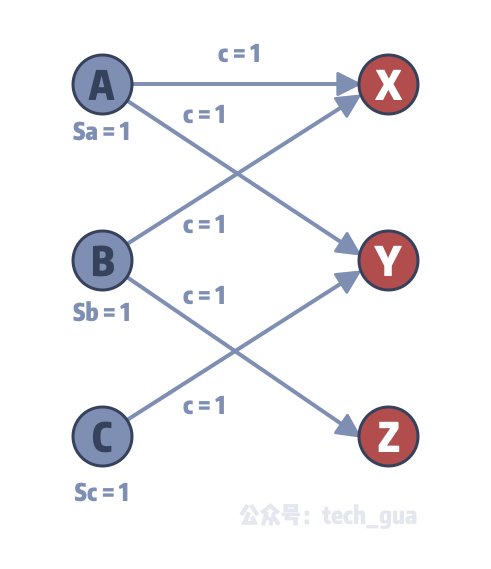
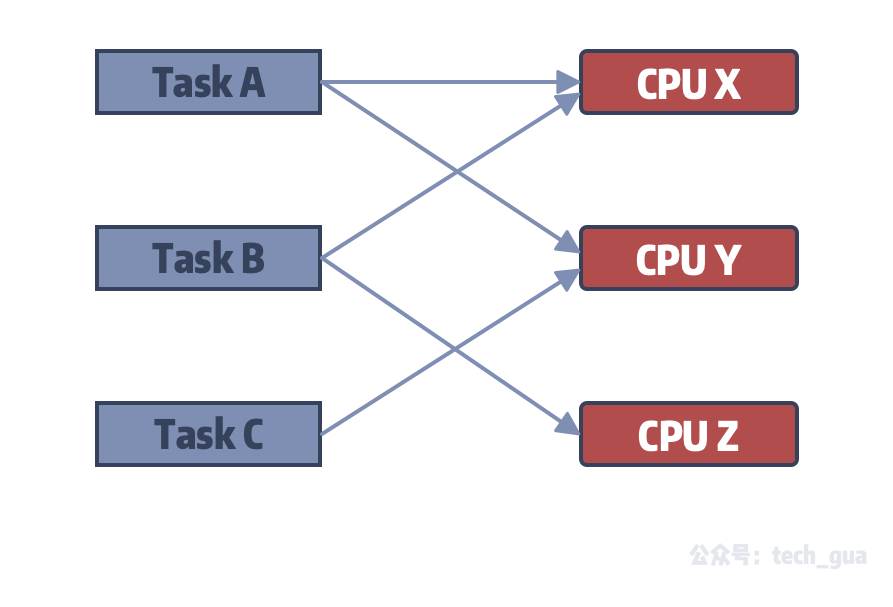
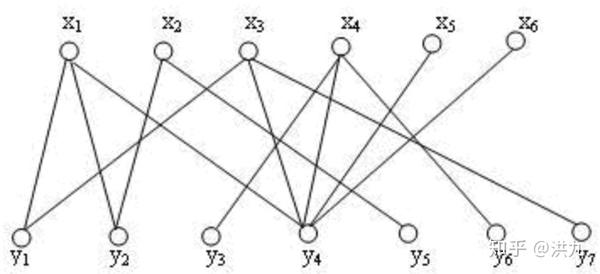
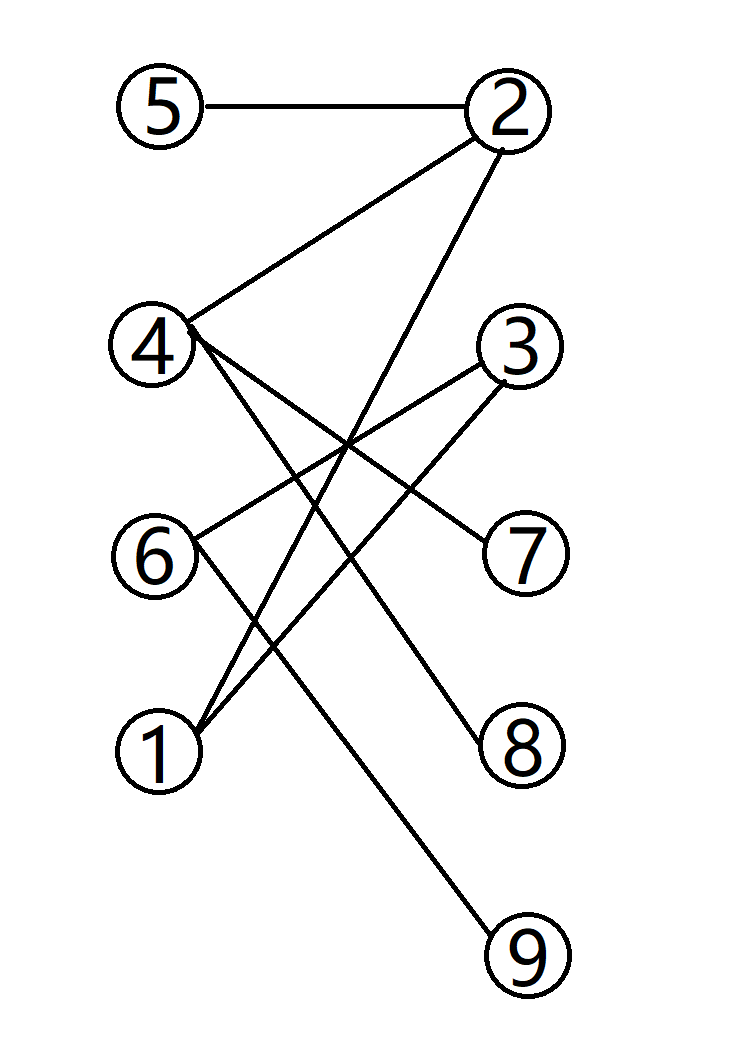
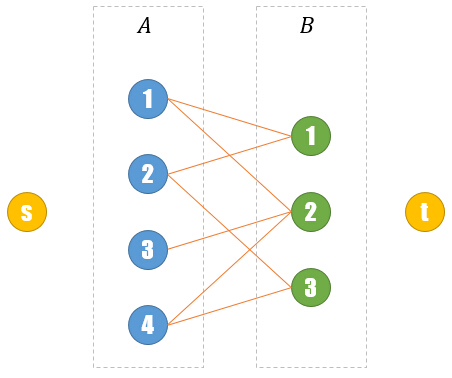
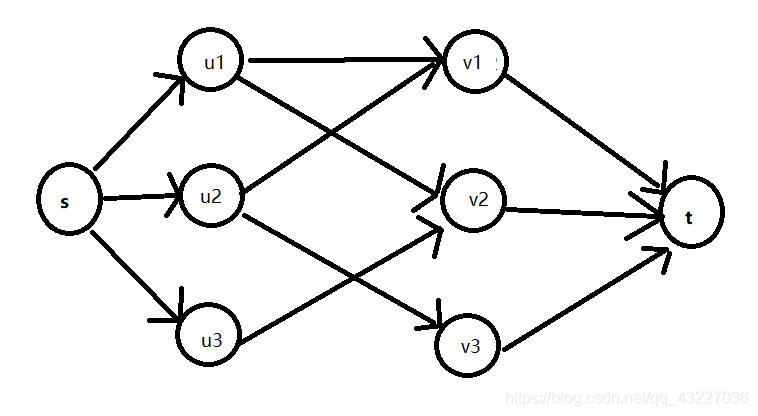
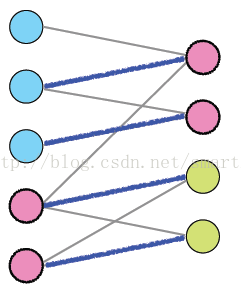
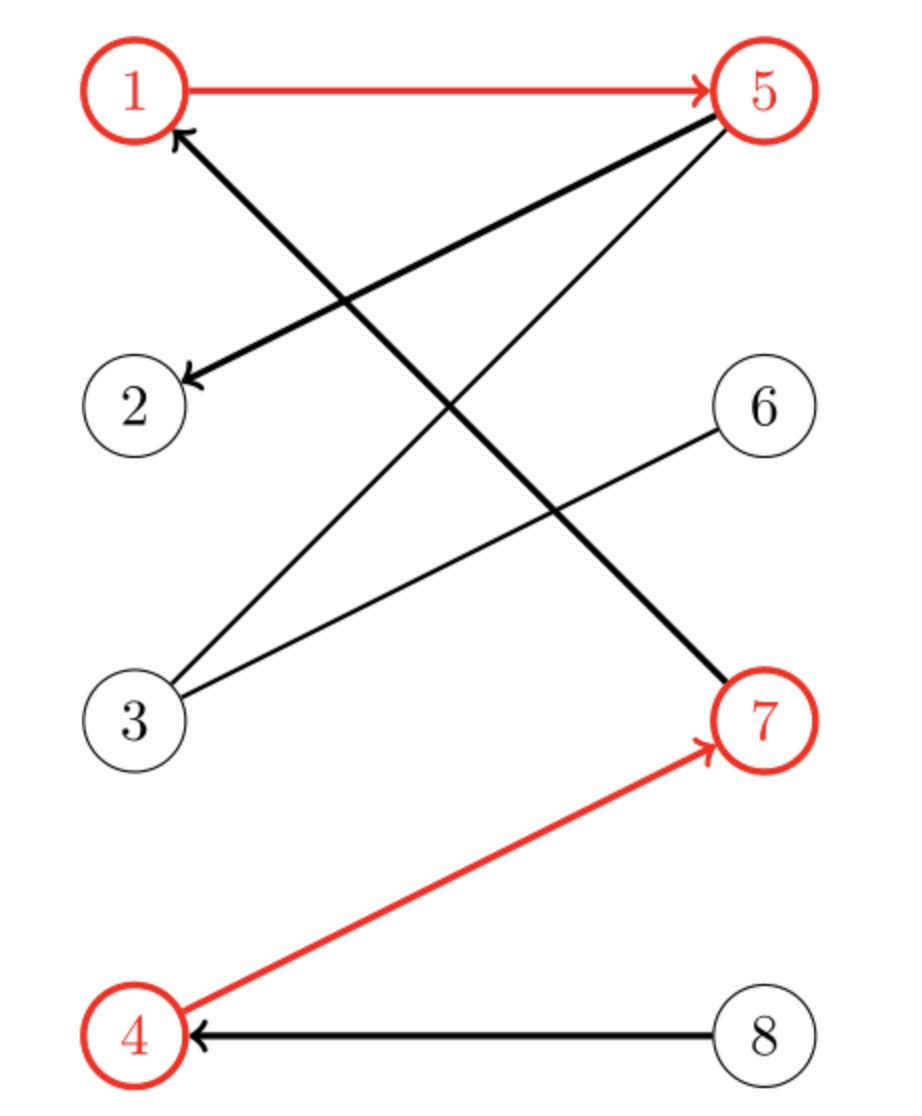
3最大二分匹配——归约到最大流问题 31 最大二分匹配问题 ( 匹配 )给定一个无向图G=(V, E),一个匹配是边的一个子集M ⊆ E,使得对于所有结点v ∈V,子集M中最多有一条边与结点v相连。
二分图 最大流-Const int MAX_V = 1e4 5;HDU 3081 Marriage Match II 最大流 之 二分图匹配 二分 HDU3605 Escape(最大流判满流 状压) HDU3081Marriage Match II (Floyd/并查集二分图匹配/最大流(二分))
二分图 最大流のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
 |  |  |
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「二分图 最大流」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
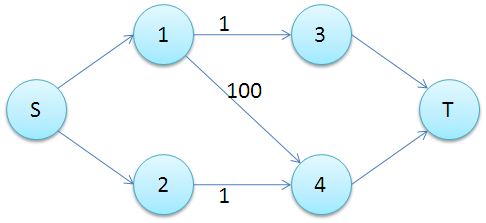 |
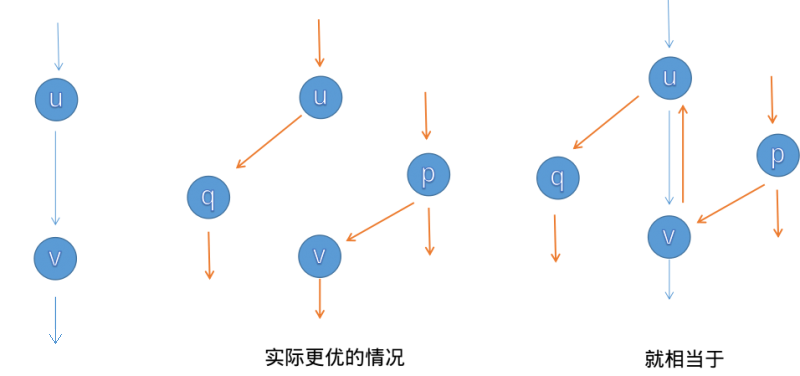
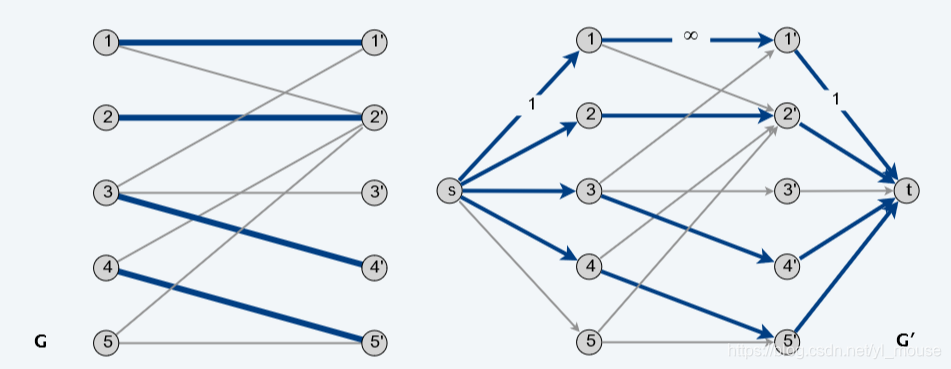
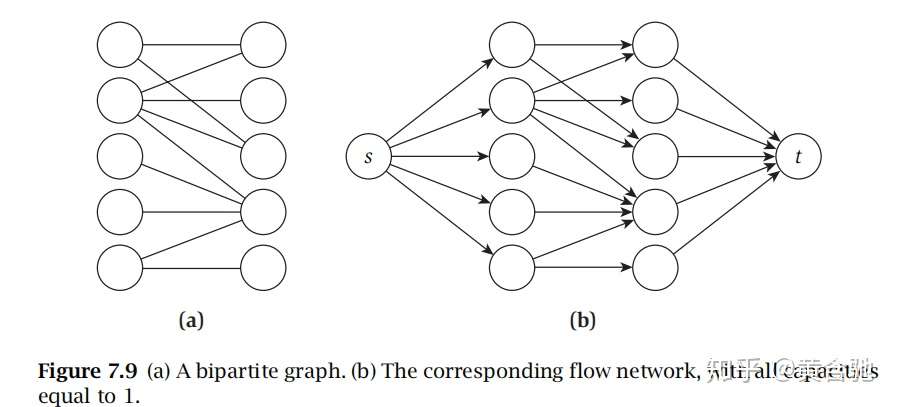
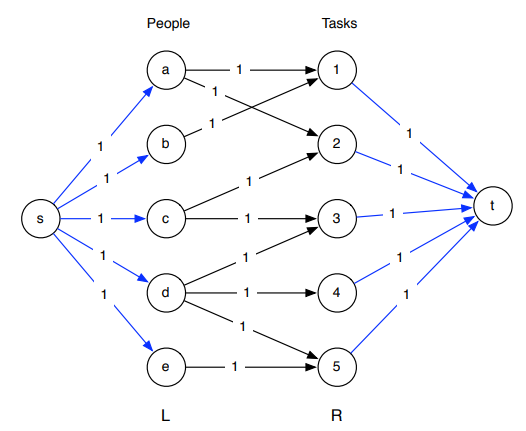
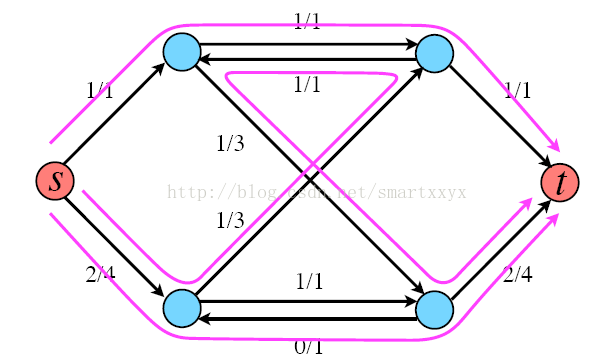
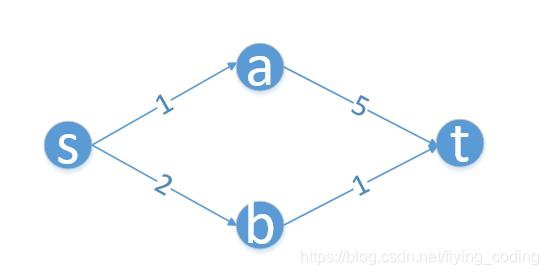
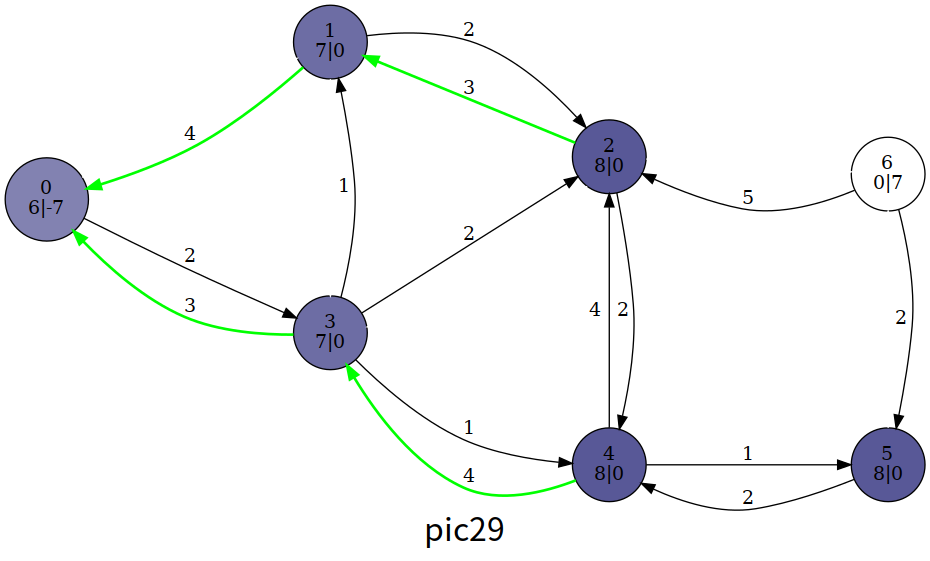
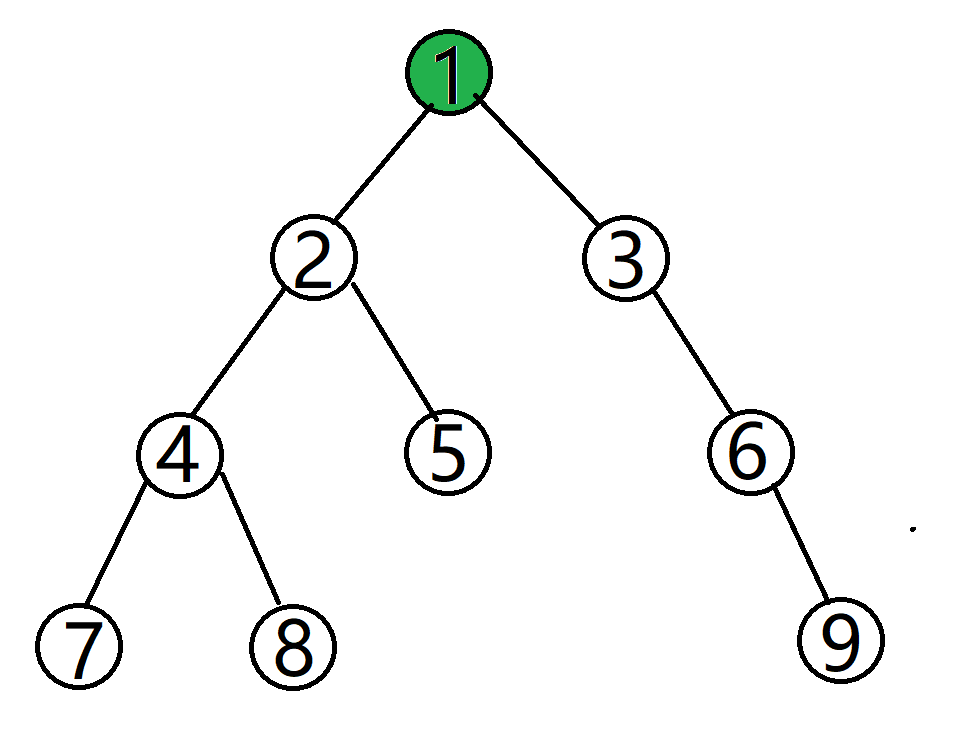
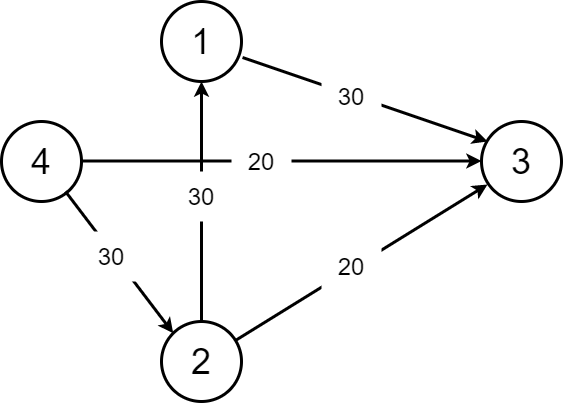
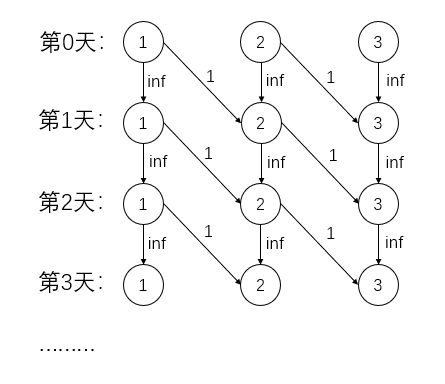
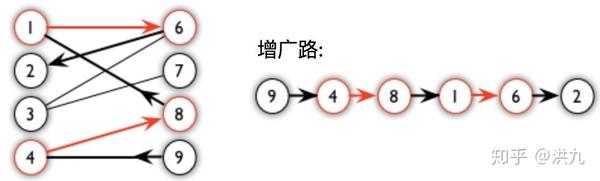
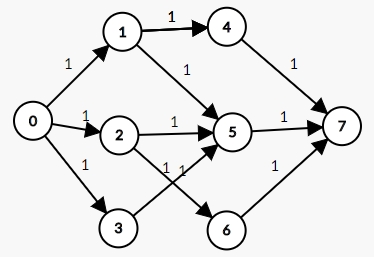
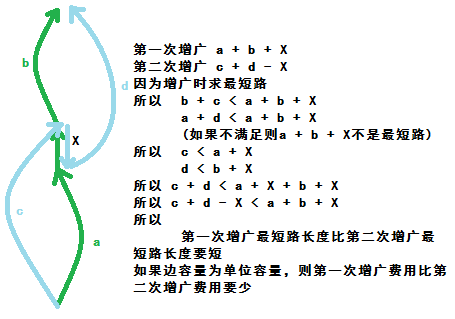
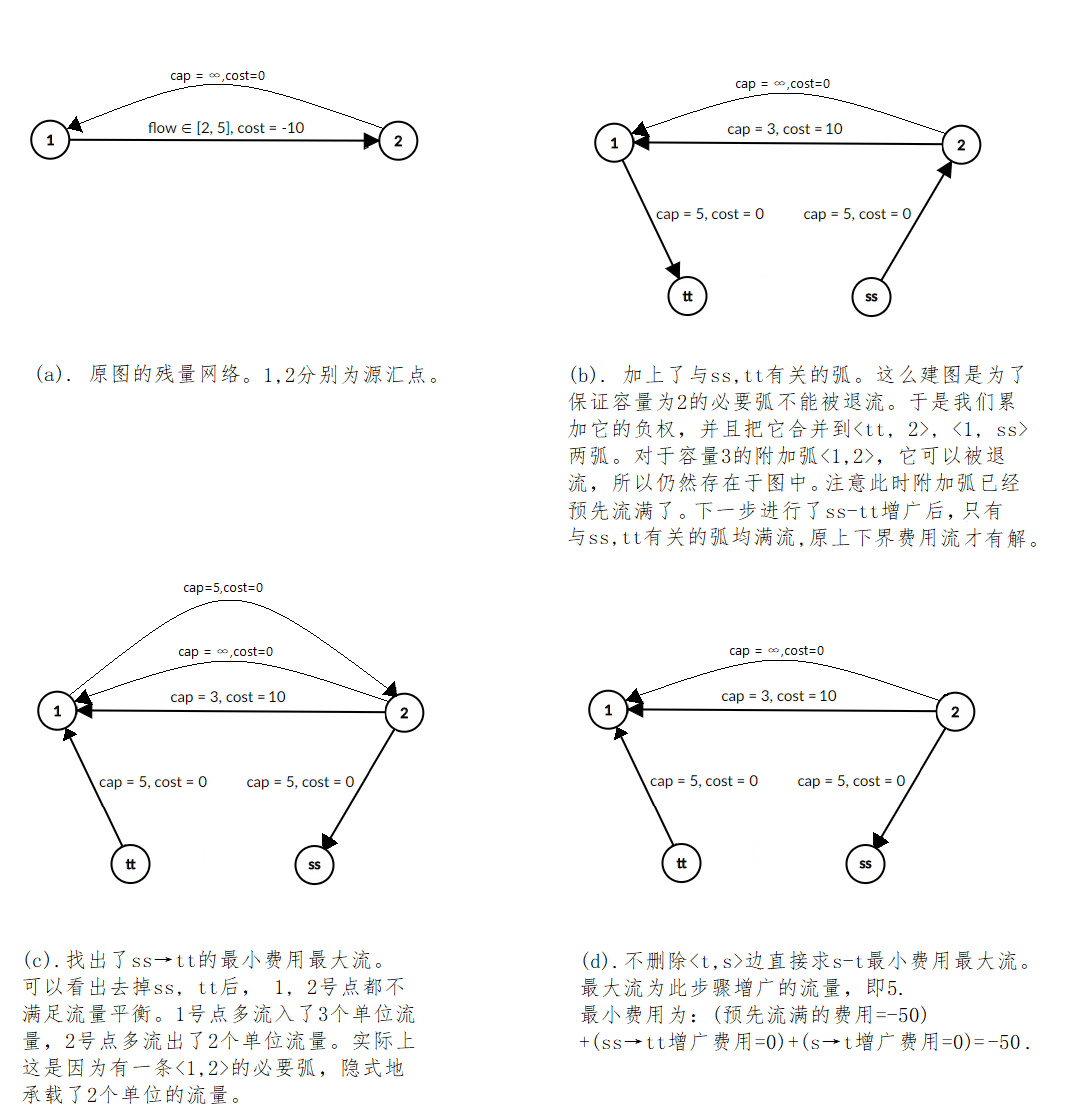
SSP(Successive Shortest Path)算法是一个贪心的算法。它的思路是每次寻找单位费用最小的增广路进行增广,直到图上不存在增广路为止。 如果图上存在单位费用为负的圈,SSP 算法正确无法求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。 、图的匹配问题与最大流问题 (五)—— 计算二分图的最大匹配 最大匹配定义:给定一个无向图 G = (V, E),一个匹配是指:E 的某个子集 M , 对于所有的结点 v ∈ V,子集 M 中最多有一条边与 v 相连,如果子集 M 中的某条边与 v 相连,那么称 v 由 M 匹配;否则 v 就是没有匹配的。
Incoming Term: 二分图 最大流,




0 件のコメント:
コメントを投稿